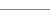
Ein Abbild ohne jede Optimierung, direkt vom Sensor ausgelesen, ist relativ flau in der Farbgebung und zeigt nicht die Texturschärfe, die man erwarten würde. Die Ursache hierfür sind charakteristische (lichtabhängige, temperatur- und zeitabhängige) Unterschiede zur natürlichen Wahrnehmung. Das Wahrnehmungsspektrum des Sensors hat im langwelligen Rotbereich sein Maximum. Das menschliche Auge kann den Grünbereich besser differenzieren. Ein Sensor muß neben der Farbwertung auch Störungssignale korrigieren, die sich als ein Gesamtrauschen (thermischer Dunkelstrom, Amp Noise usw) zum Eingangssignal hinzuaddieren. Ein kurzer Überblick soll die DIP-Grundlagen verdeutlichen.

Die vom Auge als unnatürlich empfundene Farbwertung des Sensors, das Rauschen und die flache Schärfe werden durch das Image-Processing korrigierend ausgeglichen. Die Hauptaufgaben des DIP sind die Kalibrierung der Helligkeit, die Justierung des Gammafaktors, die Korrektur der Farbwertung, die Rauschunterdrückung und die Optimierung der Schärfegradienten.

Vor dem Anwenden von Korrektur- oder Optimierungs-Filtern ist ein Werteprofil der gesamten Sensorfläche als Funktion von Ort und Lichtwert die Basis für jede weitere Berechnung. Diese Zahlenmatrix würde bei Ablichtung einer Normtafel einen individuellen "Fingerprint" des Sensors erkennen lassen, denn selbst Sensoren aus gleicher Fertigungsserie sind nie identisch und haben lokalisierbare Wertedifferenzen. Es bedarf daher einer neutralen und konstanten Bewertung der Lichtintensitäten, die dem menschlichen Auge genügen müssen. Optische Sensorik dient der Transformation für die menschlichen Wahrnehmung und sie erfüllt damit eine reproduzierende Funktion. Aber sie ermöglicht auch eine Expansion der Wahrnehmung im Sinne von Diagnostik bzw Analyse und trägt so zur Visualisierung der Natur bei. Letzterer Aspekt geht weit über den Anspruch von Urlaubsbildern hinaus und macht mit "technischen" Meßwertprofilen Ereignisse sichtbar, die ohne diese Wahnungsübersetzung verborgen bleiben.

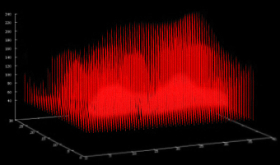
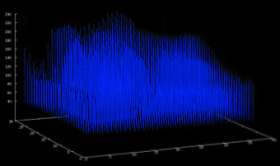
		Das Ausleseergebnis einer sensorischen Bildebene sind solche Profile. Unabhängig von der späteren Ausgabe, meistens ein RGB-Format, wird für jede Photodiode der Farbwert (Intensität, Helligkeit) und die zugehörige Position (x,y) ermittelt. Aus der Zuordnung von Orts- und dem Meßparameter für die Intensität resultiert jeweils eine 3D-Matrix, die Grundlage für das nachfolgende Image-Processing ist. Wenn der Inhalt einer Sensorebene zeitnahe optimiert werden soll, dann muß der volle Zugriff auf die Position (x,y) und den Lichtwert (c) sehr schnell erfolgen. Die Bildfolge ist also von schneller Hardware und effektiver Mathematik abhängig. Das Speicherabbild wird ausgelesen und sofort digitalisiert zur anschließenden Berechnung der Bildpixel und deren Farbwertung. Die Aufgabe übernimmt der Periferie-Prozessor mit mehreren Registerspeichern. Er schreibt die Pixel in den Bildspreicher nach Vorgabe der DIP-Operatoren. Diese scheinbar banale Tatsache ist der Vorteil von digitalen Bildern, denn hinter dem AD-Wandler gibt es innerhalb der binären Schaltzustände keine Signalverluste mehr. Ein Histogramm sieht ähnlich aus wie die Ausleseprofile, es hat dennoch nichts gemeinsam mit dieser Darstellung. Das Histogramm ist nur die Summe aller Pixel mit gleichem Farbwert, ohne die Zuordung einer Ortsposition. Auch ein Igel, der am Stromkabel knabbert, könnte so ähnlich aussehen.

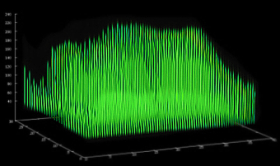
Mit der dreidimensional abgespeicherten Werte-Funktion f(x,y,c) können wir die Extrema und eine lokalisierende Steigung analytisch mit STINO-Funktionen (StInkNOrmal) berechnen - und was wir sonst noch benötigen. Die Herleitung der Basis-Funktionen ist einfacher als man bei so einer numerischen Vorgabe vermuten würde.

Obwohl man diese Thematik komplizierter dargestellen kann, bedarf es tatsächlich nur einiger Grundgedanken beim Herumspielen mit den Funktionseigenschaften, um das Prinzip zu verstehen. Man bewertet oder korrigiert die Bildpunkte durch möglichst unkomplizierte Funktionen. Die grundlegenden Filter-Funktionen lassen sich in ihrer Reihenfolge veranschaulichen:

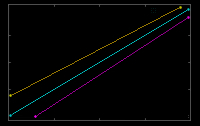
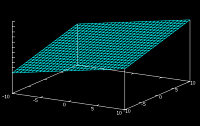
		Der einfachste Filter dient dem Helligkeitsabgleich: Diese Funktion ist eine Gerade f(x,y)= a(z+z0)+b, wobei z die Farbwertvariable ist. Sie limitiert an jedem Pixelort f(x,y) das gesamte Helligkeitsspektrum und sie kalibriert die Extrema der Farben auf den Schwarz- und den Weißpunkt. Diese Farbwert-Funktion ist ortsunabhängig, weil sie auf der (x,y)-Ebene des Sensors konstant sein muß. Eine ortabhängige Geraden-Funktion ist eine Ebene im 3D-Raum, wie etwa f(x,y)= a(x+y)+b. Sie würde auf der Sensorfläche eine kontinuierliche Änderung der Helligkeit bewirken. also eine Art Gradient-Effekt. Ein wenig Herumspielen mit den Funktionen verdeutlicht die Vorstellung zur praktischen Auswirkung.
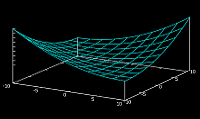
		Die Gammafunktion f(x,y) = m(z+z0)^a+b, mit einem Exponenten a>1 oder a<1, kann variabel angepaßt werden. So eine Funktion ist sowohl für die Gamma-Korrektur wie auch für die Kalibrierung der Helligkeit (wie Black/White-Balance bei Geradenfunktion) verwendbar. Die separierte Anwendung auf jeden Farbkanal ergibt den Filter für die RGB-Farbkorrektor. Als ortabhängige Exponential-Funktion erhalten wir gekrümmte Flächenprofile wie bei f(x,y) = (x+y)^a und exponentielle oder rotations-symmetrische Ortsprofile können zur lokalisierten Korrektur von optischen Störungen verwendet werden.
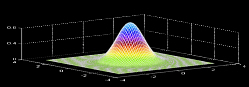
		Mit +/- a*exp(-b*x^2-c*y^2))+d erhält man schon eine dreidimensional justierbare Gauss-Funkion, die auf der (x,y)-Ebene den Ort lokalisiert und auf der z-Koordinate die Farbkorrektur enthält. Die Abarbeitung eines gekrümmten Profiles ist auf unseren dampf-betriebenen Rechnern fast so schnell (ca. +16% bei 7200x5400px) wie die einer geraden Ebene, obwohl für jede Position der Exponetialoperator abgerufen werden muß.

Die Wirkung der 2D-Funktionen kann man entweder durch Experimentieren oder mit der Gradations- oder Tonkurve in nahezu jedem Programm für Bildaufbereitung selbst austesten. Ein Beispiel zu den dreidimensionalen Ortsfunktionen f(x,y,c) wäre die Vignettirungskorrektur, die man mit einem Polynom, der Gauss-Glocke oder einfachen Quadrat-Gleichungen und ähnlichen Funktionen justieren kann.

Black/White-Balance, Gamma- und Farbkorrektur sind mit diesen handlichen Funktionen gut realisierbar. Je einfacher die Grundfunktionen, desto schneller die Belichtungsfolge. Es fehlen für ein grundlegendes Image-Processing noch die Filterfunktionen für Noise-Reduction und Sharpening. Beide Filter sind nicht realisierbar ohne die Berechnung eines lokalisierenden Gradienten.

[ weiter ... ]