Der Gradientienfilter hat die Aufgabe das Wirkungsareal für Farbwert-Funktionen als Ortsprofil zu markieren. Hört sich kompliziert an, ist es aber nicht. Den Gradientienfilter kann man sich in jedem Bildbearbeitungsprogramm ansehen, wenn man die Option "Kanten- oder Ränder suchen" bzw "vektorisieren" auswählt. Wie entsteht so ein Gradientenprofil ?

Gehen wir zunächst von einer formalen Ableitung aus, dann ist diese der Grenzwert einer Ortsdifferenz mit zugehörigem Funktionswert als Output. Der Parameter h ist der Versatz der Ortsposition.

Definieren wir für die Ableitung eine symmetrische Ortsdifferenz mit h=1, dann erhalten wir einen Gradienten für die x-Richtung zum nächsten Pixelnachbarn, also einfach die Steigung einer Verbindunggeraden zwischen (x-1) und (x+1).

Wenden wir den Gradienten auch in y-Richtung an, dann sieht die funktion so aus:

und es zerlegt sich der Gradient in zwei Komponenten jeweils für die x- und die y-Richtung.

Beides komponentenweise angewendet, wäre so etwas wie ein Nabla-Operator, der nur die Differenzwerte in beide Richtungen erzeugt. Betrachten wir p als einen Farben-Parameter, dann liefern die Ortsdifferenzen die zugehörigen Farbwerte an der Position (x_i,y_i) auf einem 2d-Ortsfeld.

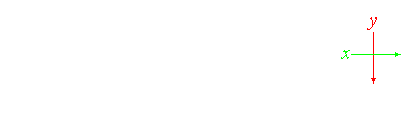
Dieser Term ist ein einfacher Kreuz-Operator und an jedem beliebigen 3x3-Ausschnitt der Bildmatrix läßt sich wiedererkennen, daß wir jetzt ein Maß haben für die richtungsabhängige Helligkeitsänderung, jeweils für zwei auseinanderliegende Pixel. Die x-Ableitung stellt demnach eine Farbdifferenz zwischen den Pixelwerten p₂₁ und p₂₃ dar, die y-Ableitung liefert die Farbdifferenz zwischen p₁₂ und p₃₂.

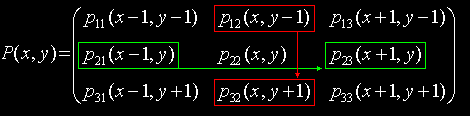
Kombiniert man die Ortsmatrix P mit Gewichtungskoeffizieten G zu p(ij)*g(ij), so führt das in Summation auf die Darstellung einer Faltungsmatrix M und mit Normierung erhält man einen Term der Form

wobei P jetzt nur noch den Ort mit Farbdifferenzwert definiert und G diesem Ort einen Gewichtungskoeffizient bzw einen Korrekturfaktor zuweist. G kann eine Funktion von (i,j) sein oder eine Konstante, mit der man beispielsweise eine symmetrische Verteilungsfunktion nachbilden kann. Der Operator M(P,G) ist auch als benutzerdefinierter Convolutionfilter bekannt, ein Matrixfeld-Filter, in dem man die Koeffizienten direkt einsetzt. Mit so einer Faltungsmatrix lassen sich die Ableitungen wiefolgt abbilden.

Die Wirkung der beiden Operatoren (dx,dy) ist auch nicht so fremd, wie es einscheinen mag. Sie entspricht der eines Relieffilters, einmal für 0° und einmal für 90°. Zur Herstellung des Gradientenprofiles ( Gradientenmaske => beide Relief-Operatoren) benötigen wir noch den Gradientenbetrag als Intensitätswert für die lokale Steigung.

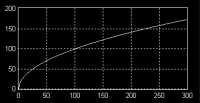
Qualitativ hochwertige Filter, verwenden andere Terme für den Intensitätswert und sehr schnelle Filter (Low Level Camera Processing) bilden nur die Betragssumme oder Geradenabschnitte.

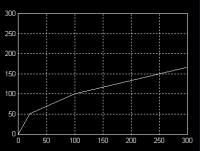Betragsgerade	Geradenabschnittsprofile
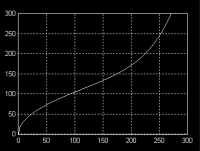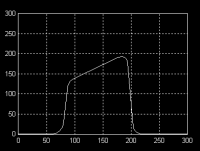Exponentialfunktionen	Exp-Bandpass-Funktionen

Damit ist der Gradientenfilter auch schon anwendbar. Die Richtungsfunktion arctan(y/x) hat als Steigungswinkel für das Sortiment der Grundfilter in der Praxis meist keine weitere Bedeutung. Komplizierter wird es erst, wenn ein besonders hohes Maß an Signalreinheit bei maximaler Verstärkung realisiert werden soll.

Nach dem Grundprinzip der Faltungsmatrix generiert die Kamera den durch das Gradientenprofil lokalisierten Sharpen-Filter. Die Bildschärfe ist dabei grundsätzlich nur eine Kontrastanhebung zweier nebeneinander liegenden Pixel. im einfachsten Fall realisiert durch eine Geradenfunktion mit Steigung m>1. Das Gradientenprofil markiert den Ort, wo die Kontrastierung erfolgen soll, und der Matrix-Operator erfüllt die Kontrastierungseigenschaft.

Ein Faltungskern K(ij), der nur im Zentrum einen positiven Koeffizienten aufweist, aber umgeben ist von nagativen Koeffizienten, erzeugt eine Kontrastverstärkung. Nagative Koeffizienten haben die Wirkung eines Inverters für den jeweiligen Pixelort in Relation zum positiv bewerteten Bildpunkt im Zentrum.

Das Gegenteil der lokalisierten Schärfe ist ein Blur- oder Smooth-Filter. Dieser Weichzeichner kann ebenfalls mit dem Convolutionfilter erzeugt werden, in dem man eine Koeffizientenverteilung wählt, die etwa der einer Gauss- oder Lorentzfunktion entspricht:

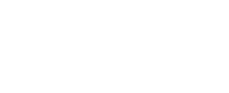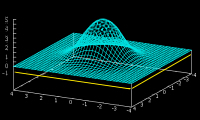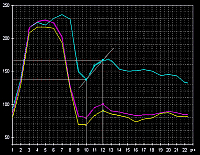
Je nach Breite der Gaussfunktion ist damit der Anteil des motivabhängigen Rauschens (Lichtverteilung, Farbdifferenz) und das thermische Rauschen (z.B. bei Langzeitbelichtung) herauszufiltern. Genaugenommen ist der "dynamische" Rauschanteil physikalisch temperatur-, zeit-, helligkeits- und farbfrequenz-abhängig, das "statische" Rauschen ist vorgegeben durch die Verstärker-Komponenten und die Fertigungspräzision des Sensors. Mathematisch aber ist die Gesamtstörung nur abhängig vom Ort und der Intensitätstoleranz. Die Gaussbreite wird auf den mittleren Abstand der Störung (Ortsfrequenz) und auf die Toleranzhöhe (Rauschpegel) abgestimmt. Der Nachteil des Gaussfilters ist ein Detailverlust in dieser Periodizität. Reduzieren kann man den Detailverlust durch Kombination des Gaussfilters mit dem invertierten Gradienten. Das Gradientenprofil als Lokalisierungsmaske wird für den Sharpen- und auch für den AntiNoise-Filter benötigt.

[ weiter ... ]